이 글은 JOYROK의 Tech Art Chronicles: What Are SDFs Anwyay? 의 번역글인 SDF가 뭔데 씹덕아!!! 에서 이어지는 글 입니다.
이번 것도 JOYROK의 글이며, Tech Art Chronicles: SDFS - Part Two의 번역글 1번째 입니다.
시작해보죠.
(주의사항: 이번 글은 읽다가 머리가 빠개질 수 있습니다. 안전에 유의하세요.)

Distance Fields
SDF에서 "S"가 없는 SDF는 있을 수 없죠!
SDF 튜토리얼 PART 1에서는 texture distance field에 대해 다루었고,
대부분의 경우 음수 값이 없기 때문에 "서명된" 것이 아니라는 점을 설명했습니다.
이는 범위를 다시 매핑하지 않으면 음수 값이 포함되지 않기 때문입니다.
그래도 텍스처를 사용해도 여전히 멋진 효과를 만들 수 있다는 것이 중요하죠.
예를 들어, 이런 것들이 가능합니다:
수학적으로 생성된 서명된 거리 필드(SDF)를 어떻게 얻을 수 있을까요?
텍스처를 전혀 사용하지 않고 거리 필드를 만들 수 있는 방법은 무엇인가요?
수학적 SDF는 텍스처 없이도 놀라운 그라데이션, 복잡한 애니메이션, 더하기/마스크 효과 등을 구현할 수 있습니다.

아래 예시들은 언리얼 엔진과 유니티에서 모두 작동하며, 두 엔진에서 어떻게 구현되는지 보여줄 것입니다.
또한 Adobe 제품을 참조하겠지만, 이를 이해하는 데 꼭 필요하지는 않습니다.
수학적으로 생성된 서명된 거리 필드(Signed Distance Fields)
먼저 기본적인 원(circle)부터 시작해 보겠습니다.
서명된 거리 필드(SDF)를 텍스처로 사용하는 것은 매우 유용하며 멋진 효과를 낼 수 있지만, 더 흥미로운 개념은 텍스처를 수학으로 대체하는 것입니다!
예를 들어, 아이콘의 배경으로 멋진 원을 만들고 싶다고 해봅시다.
전통적인 방법은 포토샵 같은 이미지 편집기에서 원을 만들고, 이를 텍스처로 저장한 후 엔진에 가져와 아이콘 아래에 배치하는 것입니다.
그러나 수학을 사용하여 원을 생성하는 방법도 있습니다.
엔진 내에서 SDF 시각화를 생성하는 이점은 크기, 그라데이션, 애니메이션, 스트로크 등을 유연하게 변경할 수 있다는 점입니다.
따라서 원 예제부터 시작해보겠습니다.
SDF와 관련하여, IQ의 웹사이트는 모든 종류의 도형을 만드는 공식을 포함하는 멋진 리소스입니다.
원을 생성하고 싶다면, IQ의 2D 원시 도형(2D primitives)에서 첫 번째 도형이 바로 원입니다:
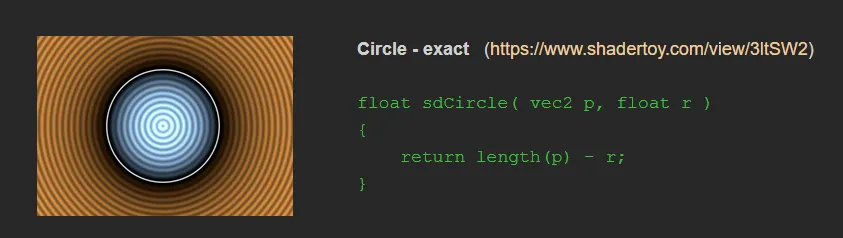
이 공식을 언리얼 또는 유니티로 변환하려면, 커스텀 HLSL 노드를 만들 필요조차 없습니다.
나중에 그 부분도 다루겠지만,
이처럼 간단한 공식에서는 UV의 길이를 구하고,
IQ의 공식에서 UV는 항상 vec2 p로 불리며,
이를 원의 크기 r에서 빼주기만 하면 됩니다.
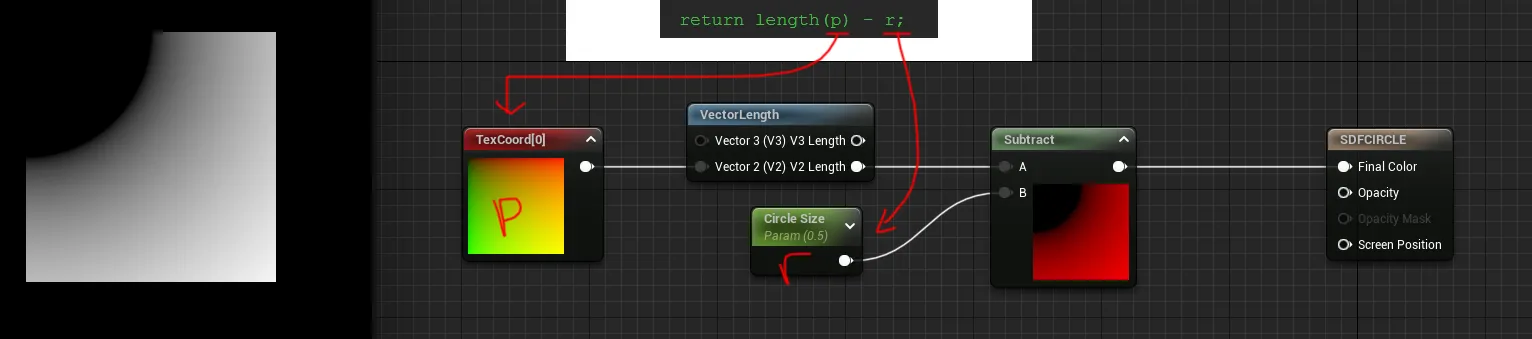
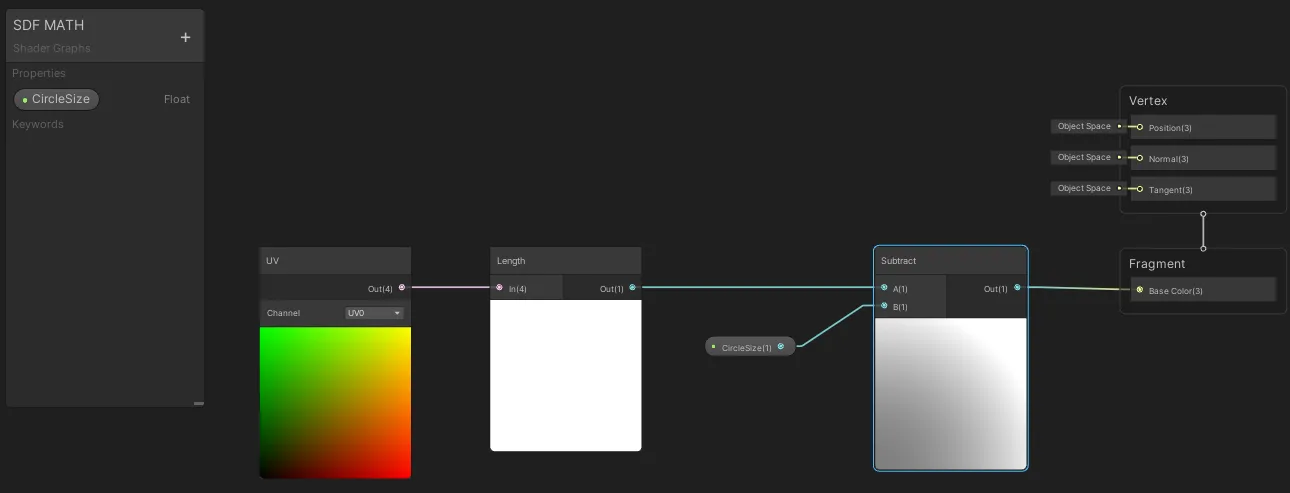
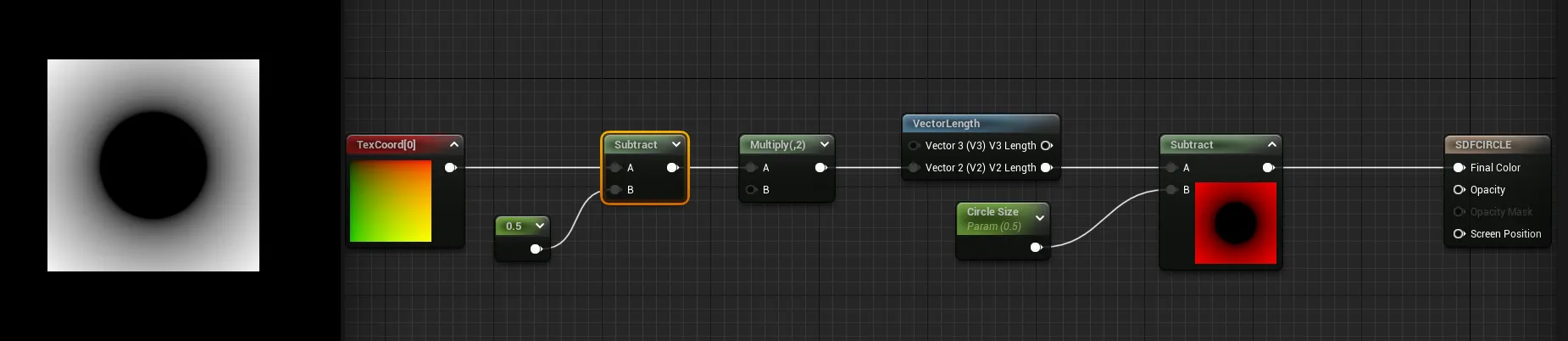
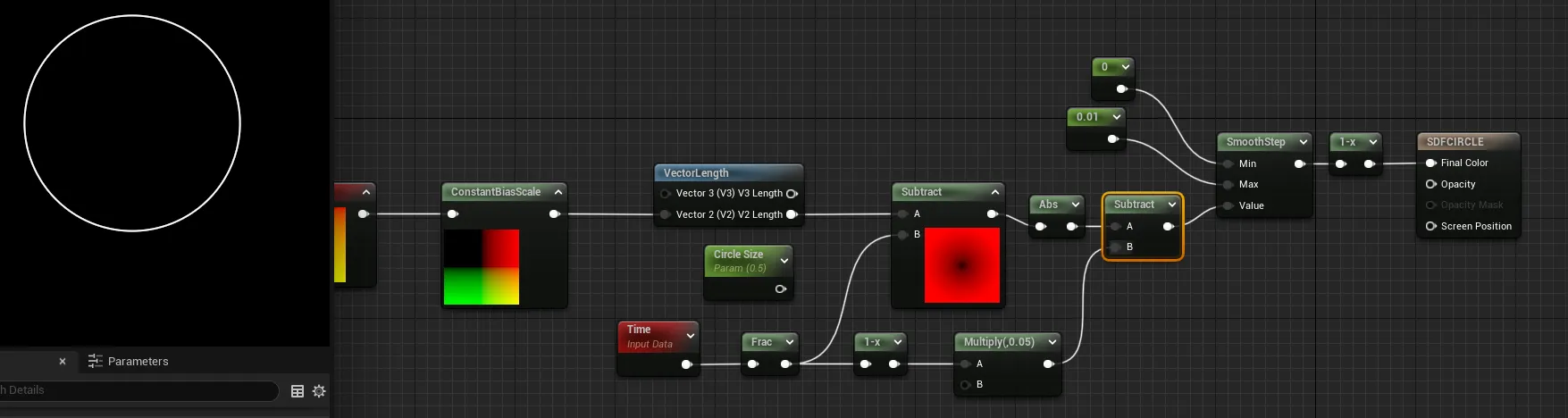
나는 IQ에서 가져온 공식을 언리얼에서 노드로 분해했습니다.
P는 TexCoord[0]이고, 그 다음에 길이를 구한 후 내가 Circle Size라고 부르는 파라미터를 빼면 원이 생성됩니다.
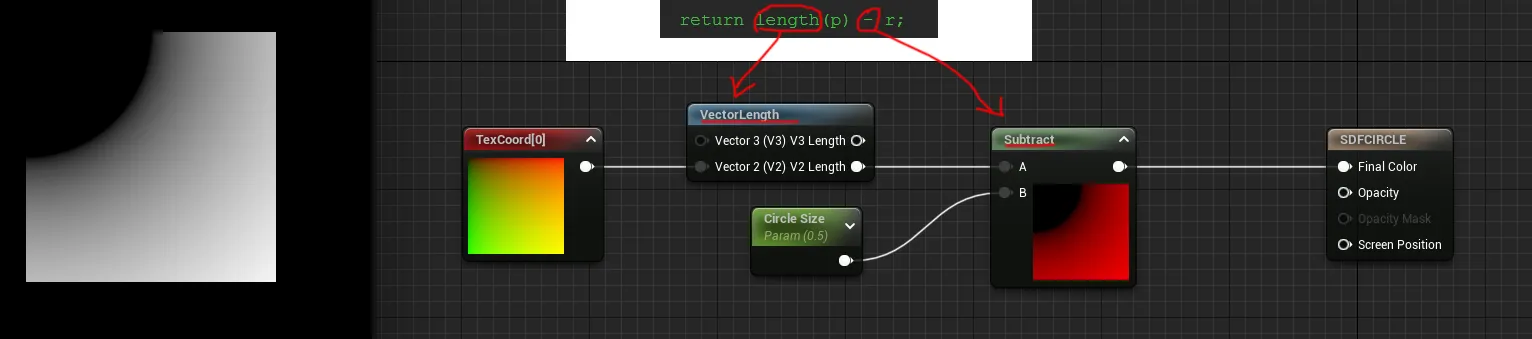
하지만 뭔가 잘못되었습니다.
원이 실제로는 재료(material)의 중앙이 아니라 왼쪽 상단에 있습니다.
이는 좌표계가 잘못된 범위에 있기 때문입니다.
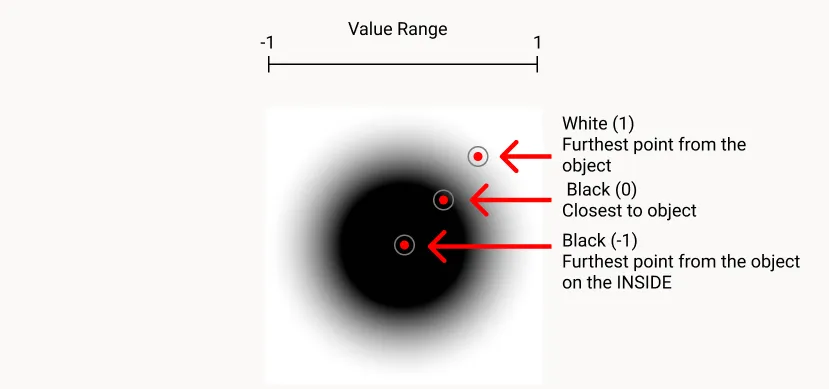
이를 설명하기 위해 간단한 다이어그램을 그려 보여드리겠습니다.

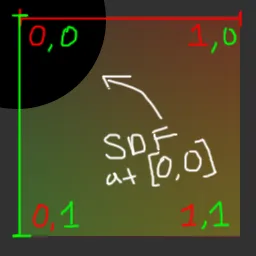
이 다이어그램에서 X축은 RED 채널을, Y축은 GREEN 채널을 나타냅니다.
따라서 이 그래프에 따르면, SDF는 중심을 [0,0]에 그리며, 반지름은 중심에서 0.5(우리의 원 크기)로 설정됩니다.
이제 재미를 위해 Unity를 살펴보면, Unity는 Y 좌표가 뒤집혀 있어서 [0,0]을 항상 왼쪽 하단에 그립니다.
따라서 Unity는 원형 SDF를 약간 다르게 그리며, 실제로 왼쪽 상단이 아닌 왼쪽 하단에 표시됩니다.
이는 UV 좌표를 살펴보면 알 수 있는데, Unity는 Y축이 아래쪽에서 0으로 시작하는 반면, Unreal은 Y축이 위쪽에서 0으로 시작하기 때문입니다.
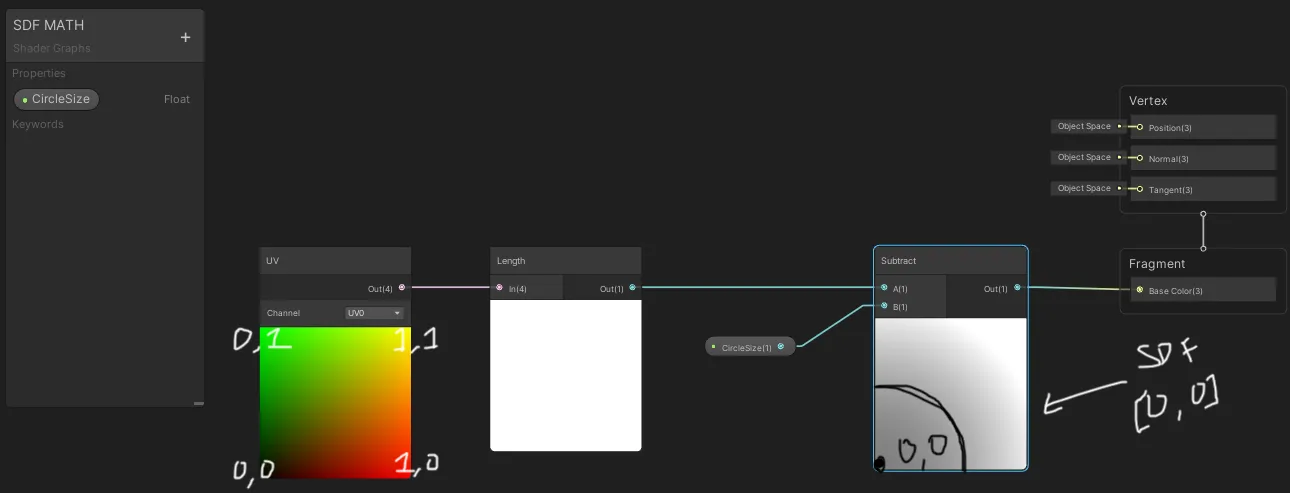
엔진에 관계없이, 좌표 시스템에서 [0,0]을 재료(Material)의 중앙에 맞추기 위해서는 좌표를 실제로 축소하고 이동시켜야 합니다.
이를 위해 UV 좌표를 조정하는 방식으로 중간에 [0,0]을 위치시킬 수 있습니다.
여기 포토샵 변환을 통해 셰이더에서 수행되는 작업을 보여주는 GIF가 있습니다:

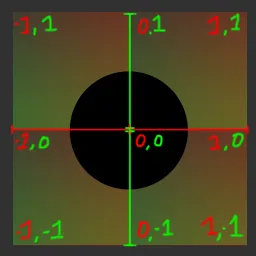
내가 수학적으로 한 작업은 0-1 범위를 -1-1로 다시 매핑한 것입니다.
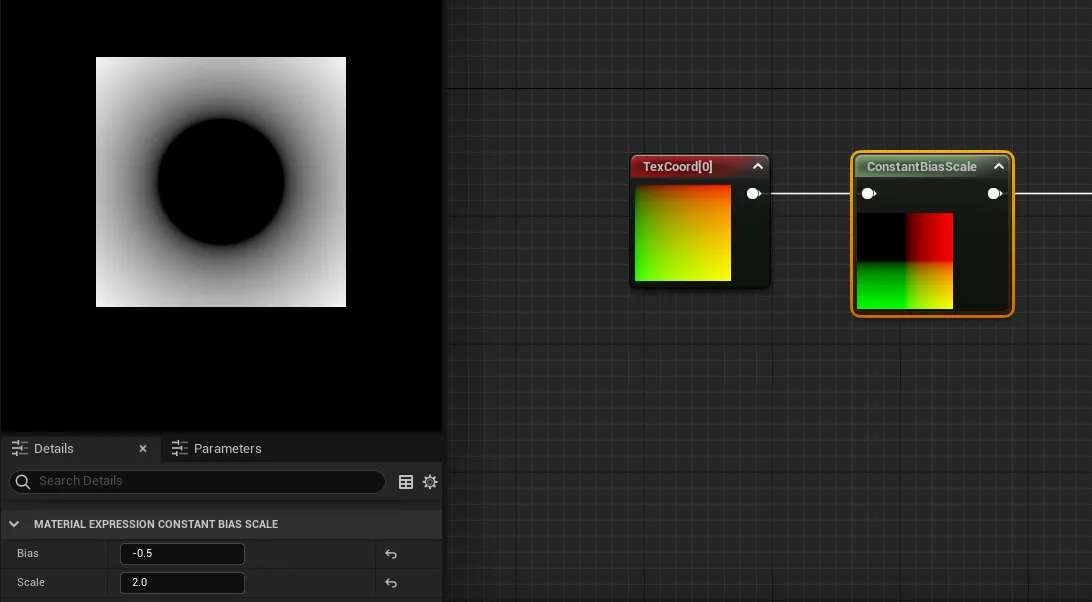
이를 위해 Constant Bias Scale이라는 개념을 사용하고 있습니다.
이 개념을 시각적으로 보여주는 그래프는 다음과 같습니다:
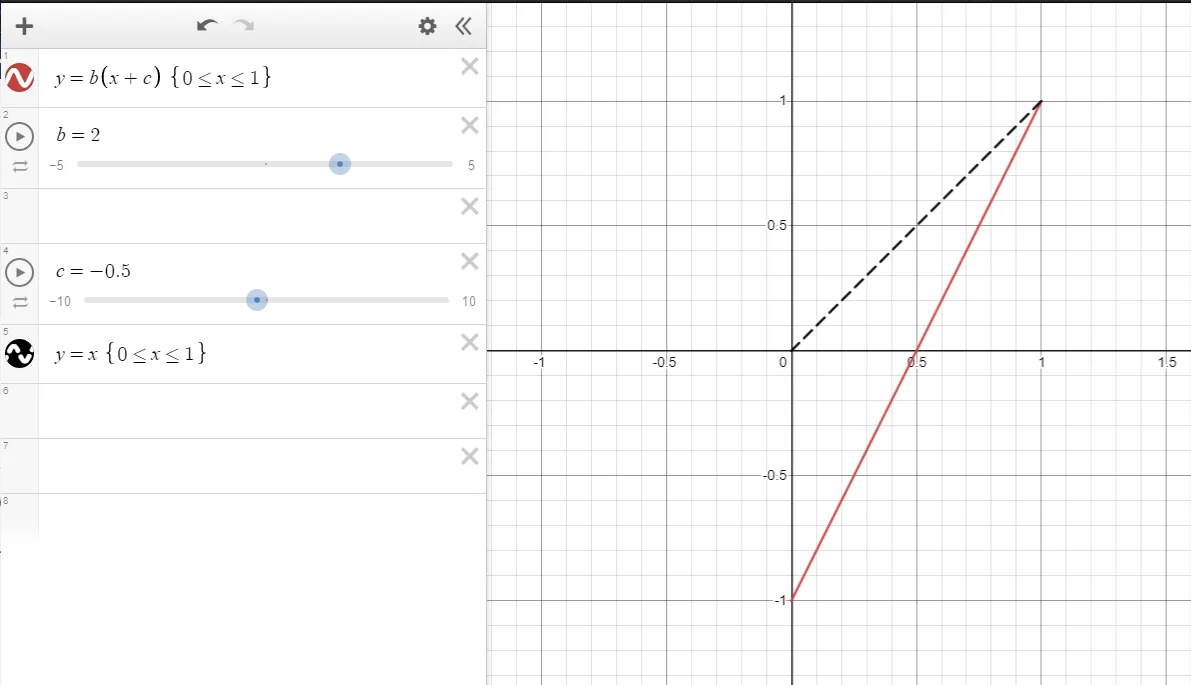
이 그래프를 보면 0-1 범위를 -1-1로 변경하려면 0.5를 빼고 2를 곱하면 됩니다.

범위를 다시 매핑하려면 단순히 2를 곱하면 0-2로 확장됩니다.
그래서 스케일링을 조정하려면 먼저 0.5를 빼야 합니다.
이렇게 하면 범위가 먼저 음수로 이동하여 -0.5에서 0.5가 되고, 그런 다음 0.5에 2를 곱하면 1이 됩니다.
이 과정은 시각적으로 수학적 변환이 어떻게 작동하는지 잘 보여줍니다.
이제 범위가 -1에서 1 사이에 있으므로 SDF는 내부 거리와 외부 거리를 나타내는 진정한 음수 값을 가질 수 있게 됩니다.
[이 개념에 대한 자세한 내용은 이전 튜토리얼을 참조하세요.]
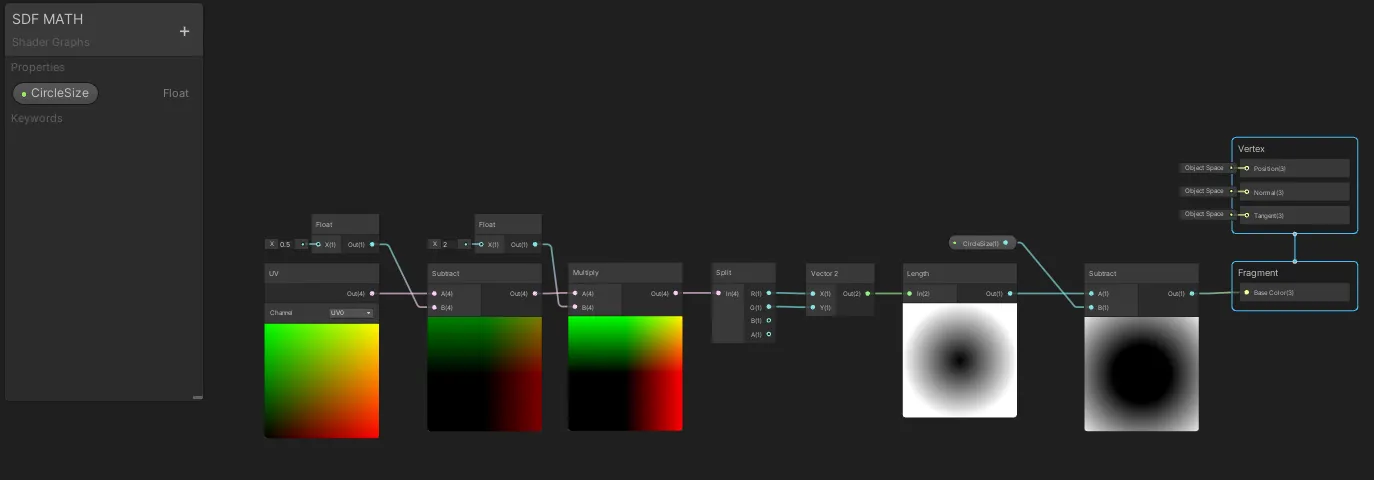
이제 언리얼 그래프에는 새로 조정된 UV 좌표 범위가 포함되었습니다.
이 범위는 빼기 노드와 곱하기 노드를 통해 설정되며, 이는 길이 계산 이전에 적용됩니다.
언리얼에는 Constant Bias Scale 노드가 있어서 빼기/더하기와 곱하기 연산을 한 번에 처리할 수 있습니다.
그래서 저는 대부분 이 노드를 사용합니다.
그리고 이것이 동일한 UV 좌표 범위를 유니티 그래프에서 다시 매핑한 것입니다:
Unity는 이 계산에서 UV를 vector2로 요구하는 경우가 많아, vector4를 vector2로 분리하는 방법을 사용했습니다.
이 부분은 아쉽지만 이번 튜토리얼의 원(circle) 예제에서는 필요했지만, 나중에 커스텀 HLSL 도형을 사용할 때는 필요하지 않습니다.
이 단계는 원을 설명하기 위해 한 것이며, 커스텀 코드 노드를 사용할 때는 필요하지 않다는 점만 기억해 주세요.
이제 수학적으로 생성된 SDF 원을 얻었습니다...
그럼 이제 이걸로 무엇을 할 수 있을까요?
텍스처 거리 필드처럼 원을 부드럽게 만들거나 덜 부드럽게 만들 수 있습니다.
기본적인 작업이지만, 이를 추가하여 원을 부드럽게 만들거나, 부드러움을 줄일 수 있습니다.
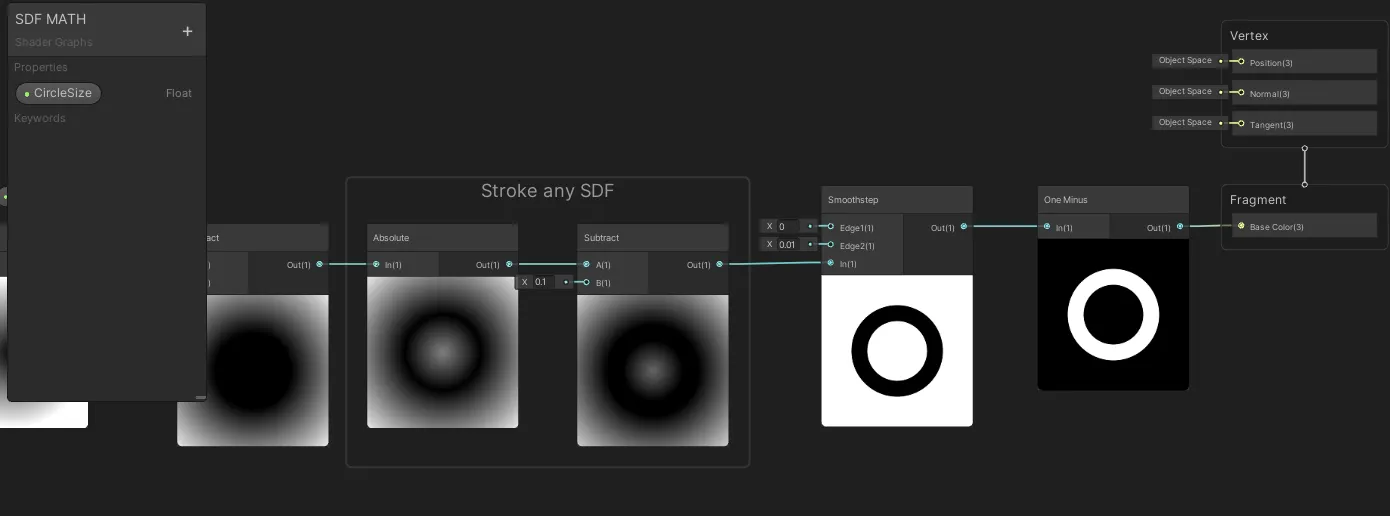
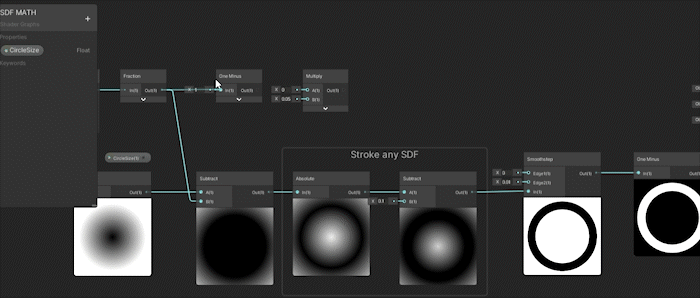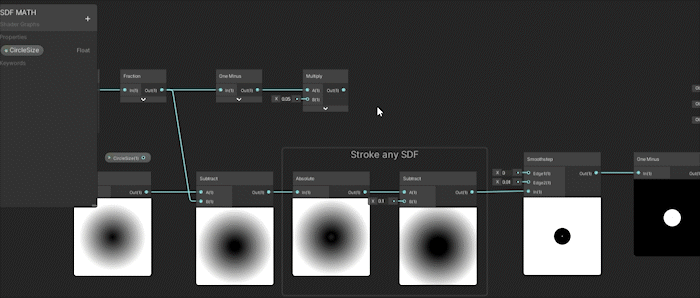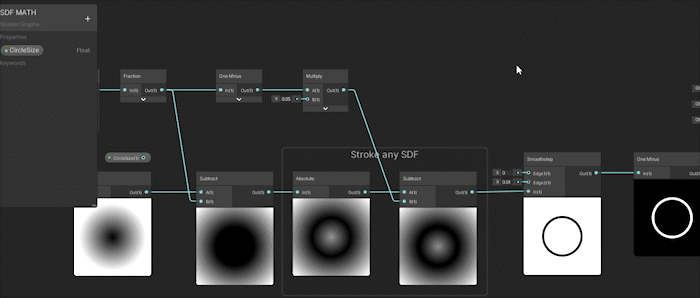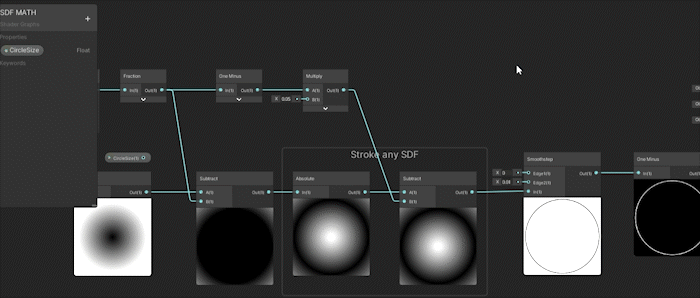
Smoothstep 노드를 추가하고 One Minus 노드를 사용하여 색상을 반전시키면, 깔끔하게 고정된 원을 만들 수 있습니다.
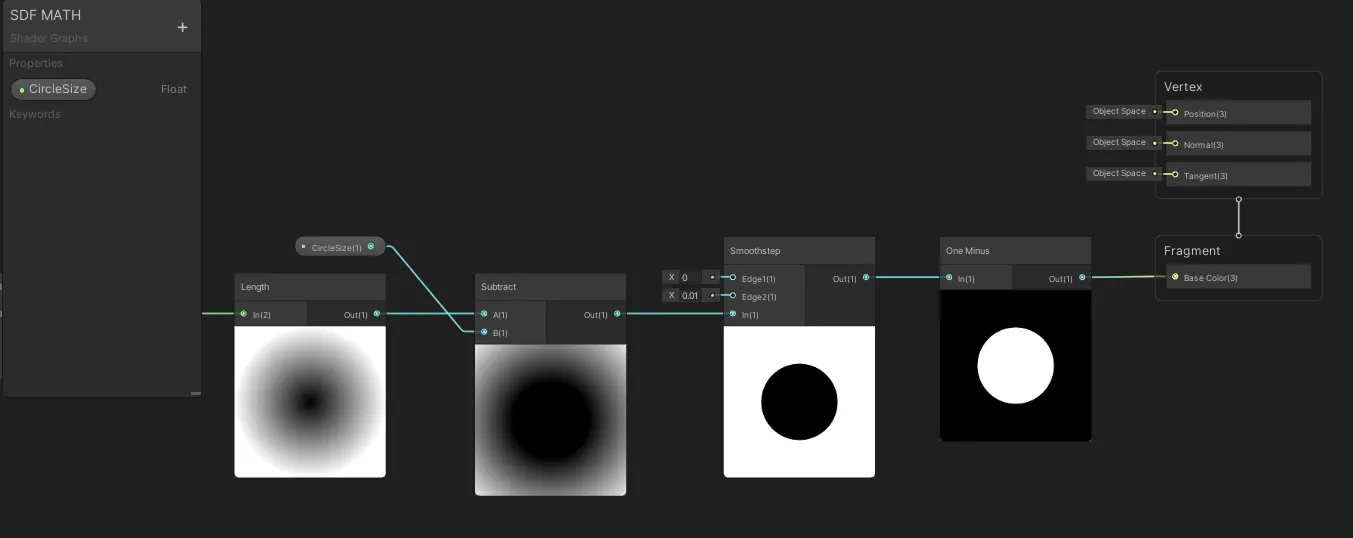
언리얼 엔진에서도 같은 개념을 적용합니다: Smoothstep 노드를 사용한 후 One Minus 노드를 통해 색상을 반전시킵니다.
제가 사용하는 Smoothstep 값은 최소값(Min): 0, 최대값(Max): 0.01입니다.
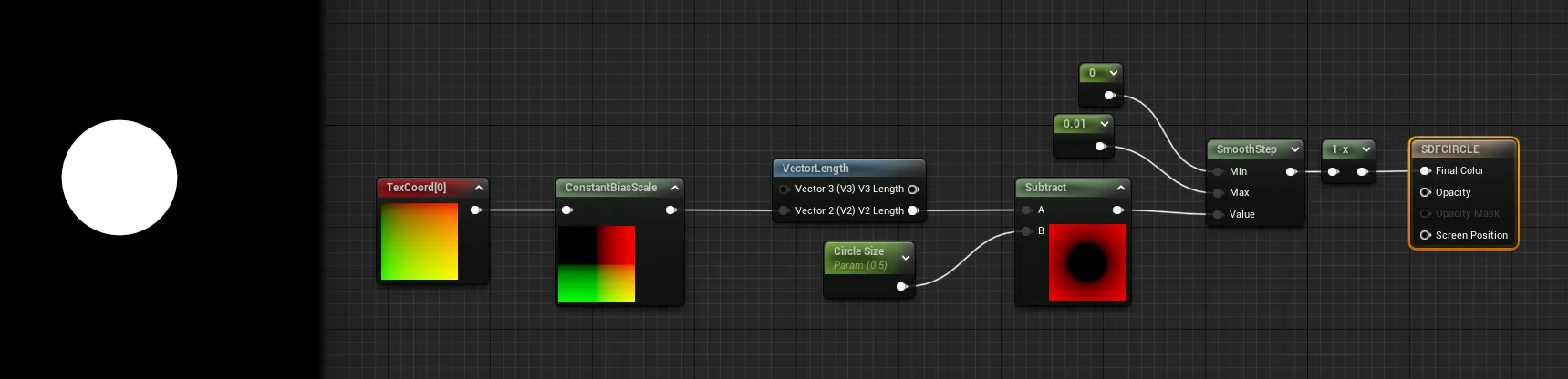
원을 애니메이션하는 방법은 간단합니다.
원 크기 값을 0.5로 설정했으니, 이를 시간(Time) 애니메이션으로 대체하면 됩니다.

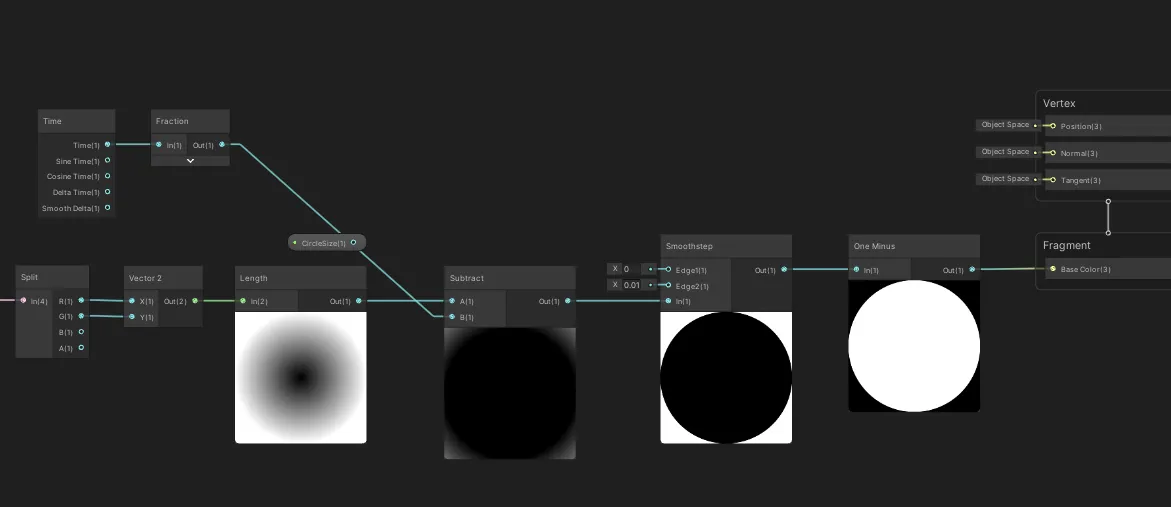
Time 노드를 Frac 노드에 연결하면 시간이 항상 0-1 사이에서 반복되도록 리셋됩니다.
이를 통해 원을 0에서 1로 확장하는 애니메이션을 쉽게 구현할 수 있습니다.
간단한 애니메이션이죠?
맞습니다!
언리얼에서도 동일한 그래프를 사용하면 됩니다.
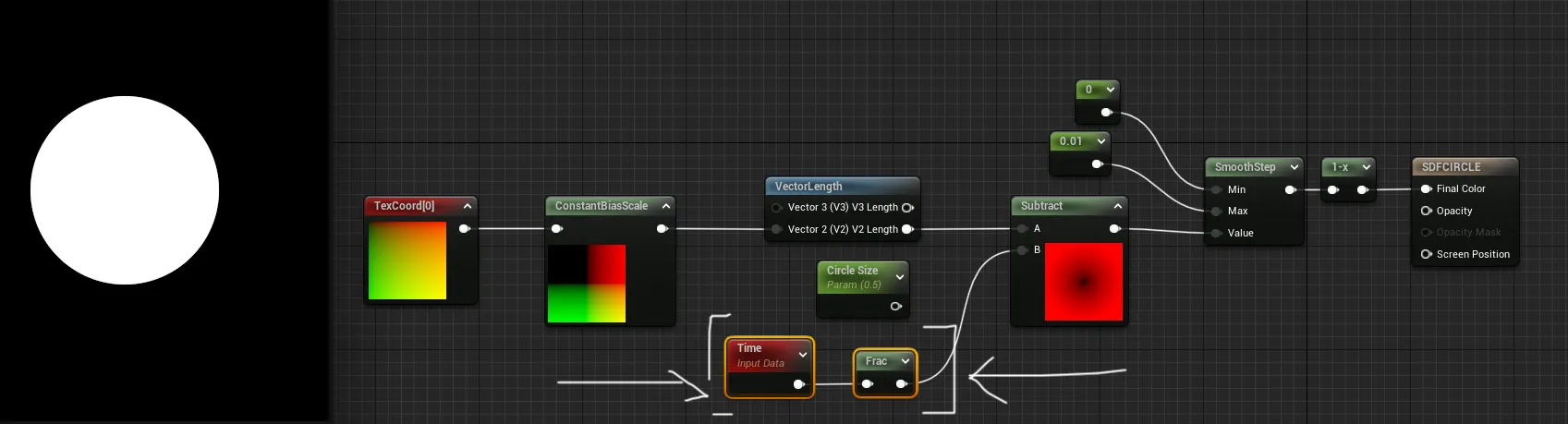
더 나아가 원을 SDF로 쉽게 스트로크된 원으로 변환할 수 있습니다...
그리고 왜 스트로크 두께를 애니메이션하지 않겠어요?
이전 SDF 튜토리얼에서 기억하듯, 절대값(Absolute) 노드를 사용한 후 빼기(Subtract) 노드로 연결하면 어떤 SDF도 스트로크할 수 있습니다.
빼기 노드의 숫자는 스트로크의 두께를 결정합니다.
이제 원의 크기를 계속 애니메이션하고, 스트로크 두께를 반대로 애니메이션한 다음, 이를 작은 범위로 곱하면 놀라운 결과를 얻을 수 있습니다.

위의 GIF에서 스트로크 두께에 연결하는 대신 Smoothstep에 잘못 연결할 뻔했습니다.
하지만 원이 커짐에 따라 스트로크 두께는 반대로 작아지고 있습니다.
이제 언리얼에서 동일한 애니메이션을 보여드리겠습니다:
이 소재는 텍스처, 추가 애니메이션, 또는 레이어를 사용하지 않고, 모든 것이 기본적인 수학으로 간단하게 이루어졌습니다...
하지만 여기서 재미가 시작됩니다!
여러 개의 SDF 수학 도형을 결합하는 것입니다!
수학적으로 생성된 서명된 거리 필드(SDF) - 도형 결합, 혼합 및 마스킹
벡터 그래픽과 비슷하게(약간...)
SDF 도형의 결합과 마스킹 부분에서는 유니티에만 집중하겠습니다.
유니티의 그래프 편집기는 기본적으로 각 노드를 애니메이션화하기 때문에, 이러한 애니메이션이 SDF의 작동 방식을 더 명확하게 보여줄 수 있기를 바랍니다.
하지만 다음 섹션의 모든 노드는 언리얼에서도 가능하니 걱정하지 마세요.
커스텀 HLSL에 들어가면 다루겠습니다.
SDF 결합하기:
SDF 도형을 결합하려면, 새로운 도형을 만들어야 합니다.
그래서 이 작은 소재에 또 다른 원을 추가하고, 이 원이 위에서 아래로 애니메이션되도록 할 것입니다.
아래의 유니티 그래프는 원이 소재의 맨 위에서 시작해 맨 아래로 애니메이션되는 방식을 보여줍니다.
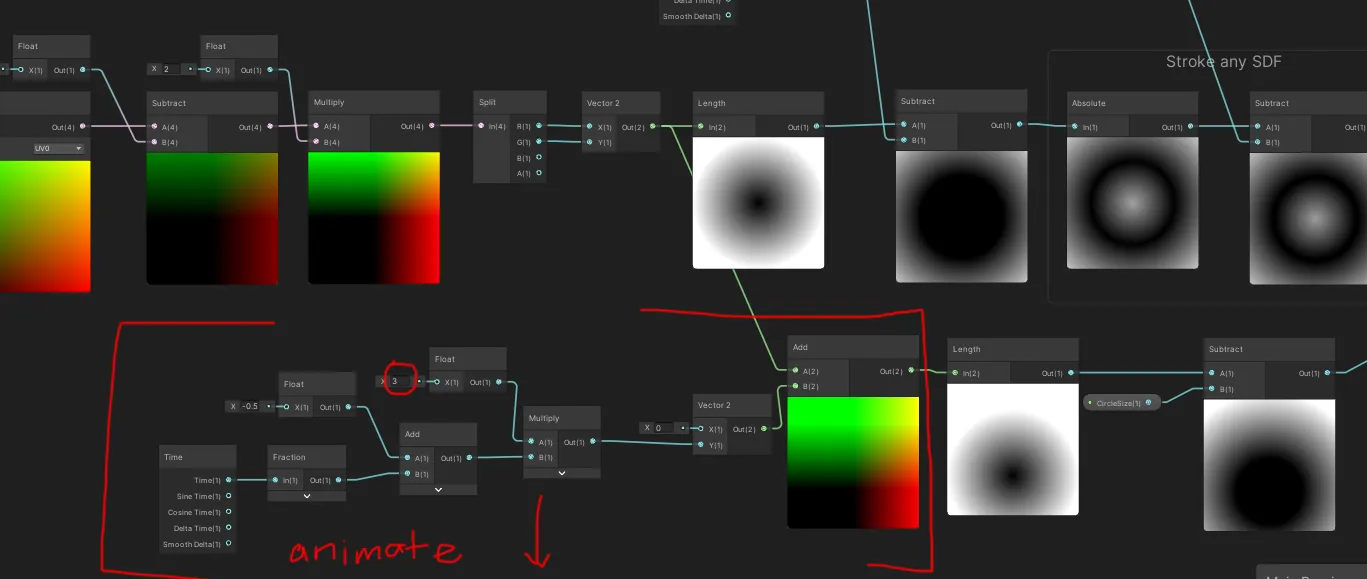
이 그래프의 작은 디테일은 곱하기 값을 3으로 변경했다는 점입니다.
이는 원이 재료 밖에서 시작하여 재료 프레임 안으로 들어갔다가, 다시 프레임 밖으로 깨끗하게 나가는 것처럼 보이도록 하기 위해서입니다.
이 설명은 조금 복잡하게 들릴 수 있지만, 실제로는 위에서 아래로 매끄럽게 스크롤되는 원으로 시각적으로 이해하기 쉽습니다.

이제 정적인 원과 위에서 아래로 스크롤되는 원을 결합하는 방법을 보여줄 수 있습니다.
이를 위해 Minimum 노드를 사용합니다:

정적인 원과 애니메이션 원을 겹치는 것처럼 생각하면 됩니다.
원을 포토샵 레이어나 애프터 이펙트 레이어처럼 겹쳐놓는 것입니다.
Minimum 노드는 이러한 원들을 결합하여 최소 값을 찾는 역할을 합니다.
내가 이해하기로는, 수학적으로는 이 결합된 SDF의 최소 값을 찾아 빠르게 분기하는 방식으로 작동합니다.
SDF 마스킹하기:
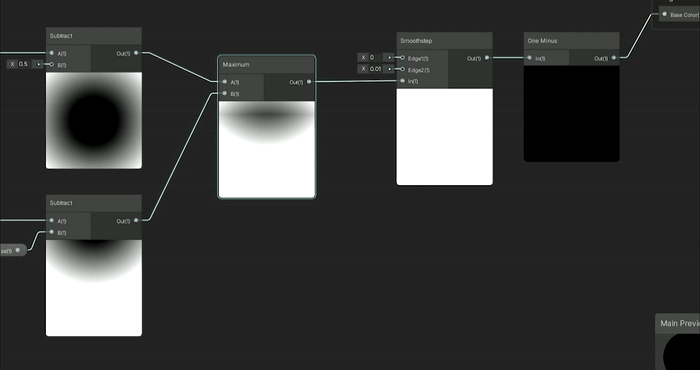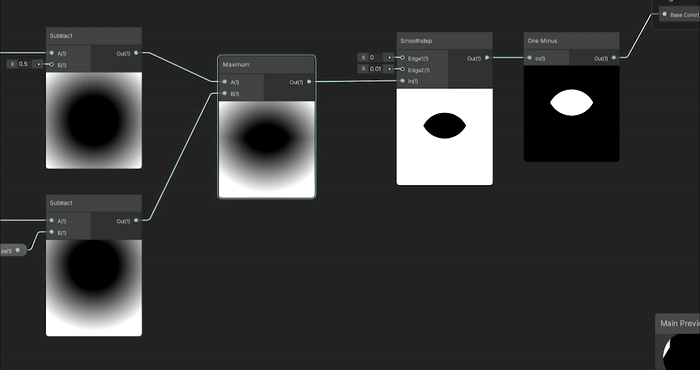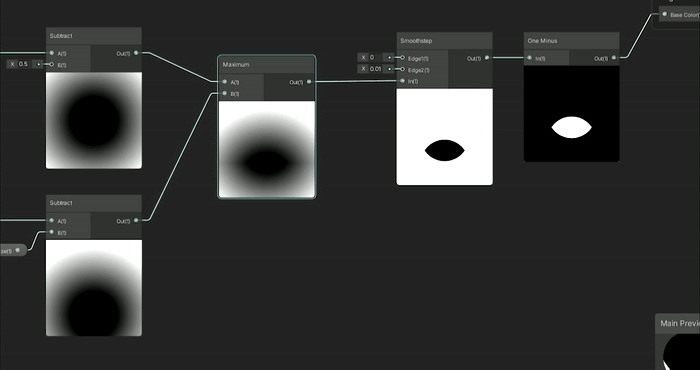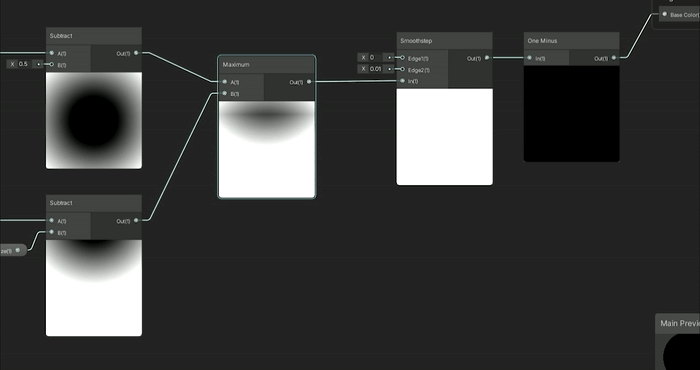
SDF를 결합하기 위해 Minimum 노드를 사용했다면, SDF를 마스킹하기 위해서는 Maximum 노드를 사용하는 것이 당연할 것입니다.
다른 IQ 기사에서 3D SDF에 대한 내용을 참고하여, 이 기사에는 합집합(Union), 차집합(Subtraction), 교집합(Intersection) 섹션이 있습니다.
이 기사는 3D SDF의 예시를 보여주지만, 2D SDF에도 적용됩니다.그래서 이 개념을 사용하여 SDF 도형을 마스킹하고 교차시킬 것입니다.

차집합은 SDF의 음수 값을 가져와 두 번째 SDF와 함께 Maximum 노드를 통과시키는 것입니다.
교집합은 두 SDF 간의 Maximum 노드를 사용하는 것으로 간단합니다.
이러한 차이점을 보여드릴 예정이니, 일러스트레이터나 포토샵의 패스파인더 도구를 사용하는 사람은 이러한 개념을 직관적으로 이해할 수 있을 것입니다.
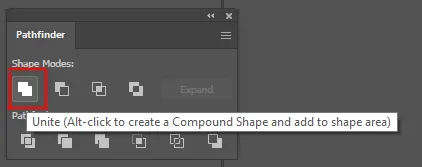
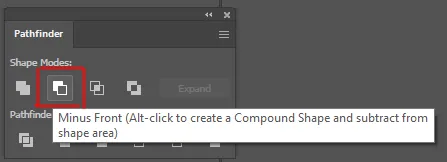
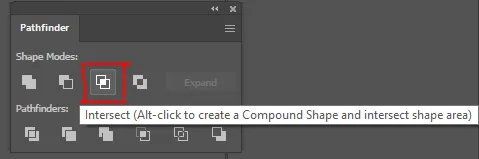
이것은 일러스트레이터의 스크린샷으로, 패스파인더 도형 도구인 Unite, Minus Front(차집합), Intersect를 보여줍니다.
이러한 아이콘들은 SDF 조합으로 인해 도형이 시각적으로 어떻게 변하는지를 보여주는 데 유용합니다!
이제 Minus Front 또는 차집합에 대해 알아보겠습니다!
이를 위해서는 max(-d1, d2)를 사용하면 됩니다.
SDF를 Negate 노드에 통과시켜 음수로 만든 후, 이 음수 SDF가 두 번째 SDF에서 차감되는 방식으로 Maximum 노드에 넣으면 됩니다.
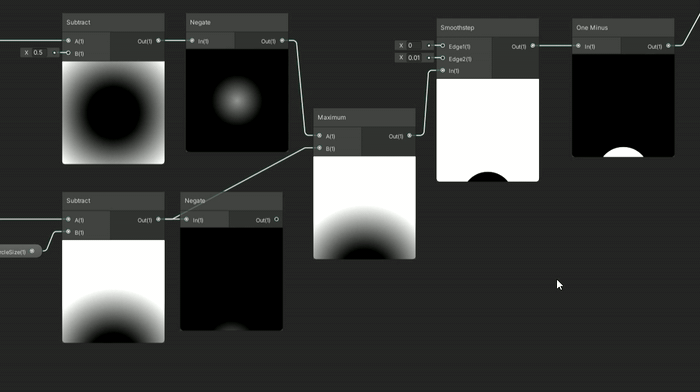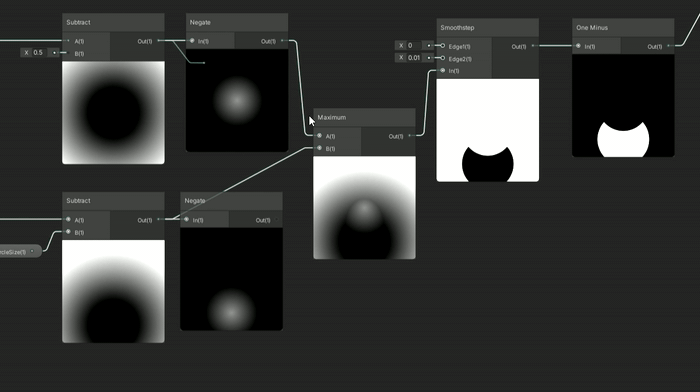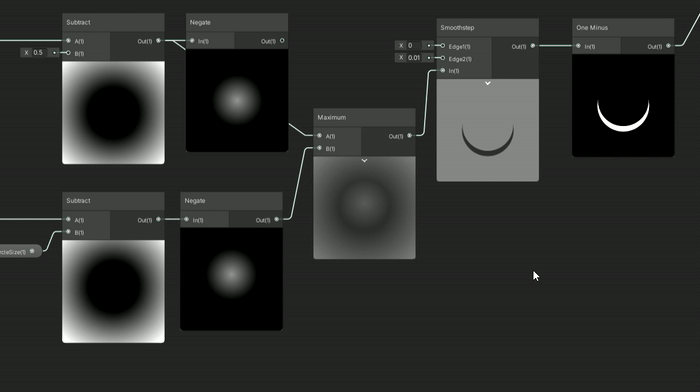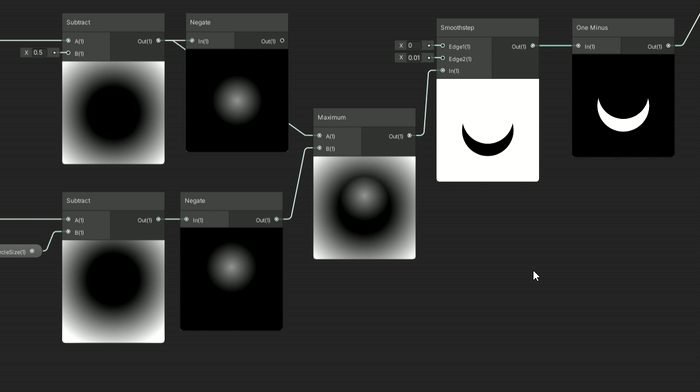
어떤 도형을 앞에 두고 싶은지에 따라, 아래 있는 도형에서 빼기 위해 음수로 만들어야 할 도형이 결정됩니다.
만약 정적인 원이 애니메이션 원에서 차감하도록 하고 싶다면, 정적인 원을 음수 SDF로 만들어야 합니다.
반대로 애니메이션 원이 정적인 원에서 차감하도록 하려면, 애니메이션 원을 음수로 만들고(negate 노드 사용), 이를 Maximum 노드에 통과시켜야 합니다.
흥미로운 점은 이 두 원을 사용한 다른 차집합 방식으로 재미있는 달/일식 애니메이션을 만들 수 있다는 것입니다.
정적인 원이 애니메이션 원에서 차감될 때, 달이 태양을 가리는 형태로 일식 같은 효과가 나옵니다.
반면, 다른 차집합 방식은 달이 주기를 거치는 모습처럼 보입니다.


두 SDF 중 어떤 것이 음수인지에 따라 Maximum 노드에 넣기 전에 마스킹 효과가 변화하는 것을 보는 것은 재미있습니다!
차집합을 위한 설정이 약간 복잡했지만, 교집합은 훨씬 간단합니다.
교집합은 단순히 두 SDF 간의 Maximum 노드이며, 이 노드를 사용하면 두 도형이 교차하는 부분만 표시됩니다.
IQ에서 제공하는 부드러운 합집합, 차집합, 교집합 수식도 있지만, 이 기사에서는 그 부분을 다루지 않겠습니다.
대신, 일러스트레이터의 패스파인더 도구처럼 SDF 도형을 합치고, 차감하고, 교차할 수 있다는 점을 다시 강조하고 싶습니다.


합집합 (Unite): min(SDF1, SDF2)


차집합 (Subtraction): max(-SDF1, SDF2)


교집합 (Intersection): max(SDF1, SDF2)
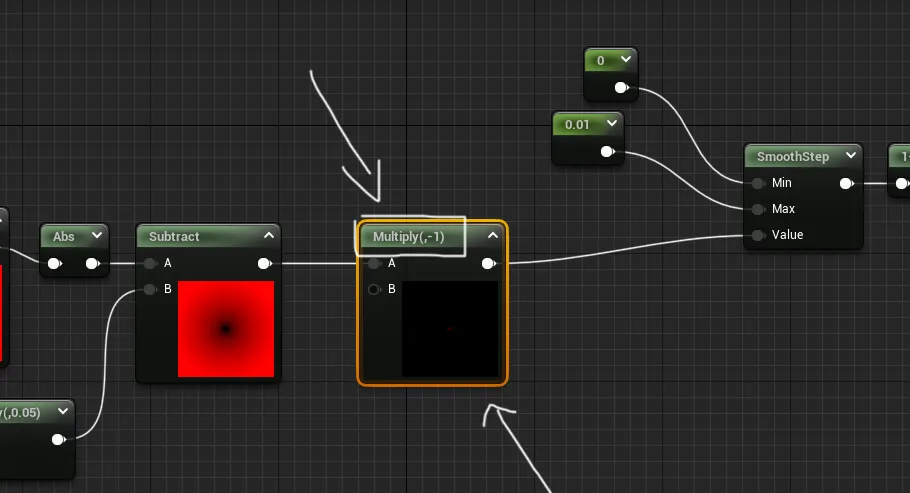
간단한 참고 사항으로, 언리얼에서는 제가 아는 한 Negate 노드가 없으므로, SDF에 -1을 곱하면 됩니다.
이미지 제한으로 2편에서 계속됩니다.