러브라이브 선샤인 마이너 갤러리 저장소

이미 누가 전에 계산해서 올린 게 있지만 https://gall.dcinside.com/mgallery/board/view/?id=sunshine&no=3186879

저 글이 올라왔을 당시엔 금카롱이 교환소랑 빅라이브엔 없었다.

이 분석글의 마지막 결론을 보면

색카롱

1카롱: 빅라이브

2카롱: 교환소 or 빅라이브

3카롱: 교환소 (or 빅라이브)

은카롱

1카롱: 빅라이브

2카롱: 교환소 (or 빅라이브)

3카롱: 교환소

노트: 무조건 샤이닝피스

화분: 교환소 or 빅라이브

4. 샤이닝피스는 걍 "노트"나 "금12카롱"으로 바꿔먹으셈. 굳이 색카롱하고 바꾸겠다면 3카롱만은 하지마셈

교환소 이벤트 재화는 "3카롱", 2카롱, 화분 추천

빅라이브 골드는 "1카롱", 2카롱, 화분 추천

이렇게 정리해놓고 있다.

여기서부터 본론인데, 내가 수학을 못해서 저 분석 내용을 봐도 이해가 잘 안 되더라고.

그래서 안 돌아가는 머리를 최대한 굴려가면서 손으로 차근차근 계산해보기로 했다.

아래는 직접 보면서 정리한 표. (소수점 아래 셋째 자리에서 반올림)

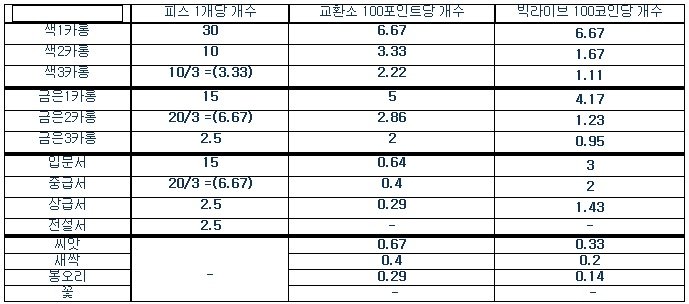
일단 계산 없이 이 표만 보고 알 수 있는 건

1. 꽃은 아무 데서도 안 파니 합숙이나 이벤트 보상으로만 얻을 수 있다.

2. 전설의 서는 샤이닝피스로밖에 살 수 없다.

근데 꽃도 전설의 서도 사용처는 페스울 뿐이니 극히 한정되어 있는데, 합숙에서 드랍률이 낮은 것도 아니라서 다들 남아도니까 굳이 교환소에서 바꿀 사람은 없겠지.

일단 위의 표에서 나온 값을 하나로 통일시키기 위해서 색 1카롱을 기준으로 잡고 값을 통일시켰다. 꽃이랑 전설의 서는 필요 없을 것 같아서 제외.

거듭 말하지만 난 수학을 못해서 이 작업하는데 시간 엄청나게 잡아먹었음.

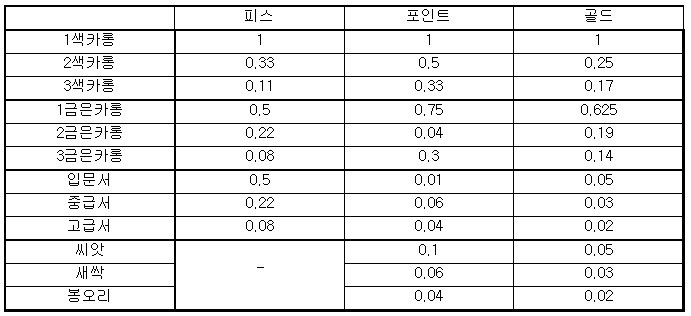
1색카롱 1개 살 만큼의
피스로 2색카롱 0.33개
포인트로 2색카롱 0.5개
골드로 2색카롱 0.25개를 살 수 있다.
1. 포인트 2. 피스 3. 골드

1색카롱 1개 살 만큼의
피스로 3색카롱 0.11개
포인트로 3색카롱 0.33개
골드로 3색카롱 0.17개를 살 수 있다.
1. 포인트 2. 골드 3. 피스

1색카롱 1개 살 만큼의
피스로 1금은카롱 0.5개
포인트로 1금은카롱 0.75개
골드로 1금은카롱 0.625개를 살 수 있다.
1. 포인트 2. 골드 3. 피스

1색카롱 1개 살 만큼의
피스로 2금은카롱 0.22개
포인트로 2금은카롱 0.04개
골드로 2금은카롱 0.19개를 살 수 있다.
1. 피스 2. 골드 3. 포인트

1색카롱 1개 살 만큼의
피스로 3금은카롱 0.08개
포인트로 3금은카롱 0.3개
골드로 3금은카롱 0.14개를 살 수 있다.
1. 포인트 2. 골드 3. 피스

1색카롱 1개 살 만큼의
피스로 입문서 0.5개
포인트로 입문서 0.01개
골드로 0.05개를 살 수 있다.
1. 피스 2. 골드 3. 포인트

1색카롱 1개 살 만큼의
피스로 중급서 0.22개
포인트로 중급서 0.06개
골드로 중급서 0.03개를 살 수 있다.
1. 피스 2. 포인트 3. 골드

1색카롱 1개 살 만큼의
피스로 고급서 0.08개
포인트로 고급서 0.04개
골드로 고급서 0.02개를 살 수 있다.
1. 피스 2. 포인트 3. 골드

1색카롱 1개 살 만큼의
포인트로 씨앗 0.1개
골드로 씨앗 0.05개를 살 수 있다.
1. 포인트 2. 골드

1색카롱 1개 살 만큼의
포인트로 새싹 0.06개
골드로 새싹 0.03개를 살 수 있다.
1. 포인트 2. 골드

1색카롱 1개 살 만큼의
포인트로 봉오리 0.04개
골드로 봉오리 0.02개를 살 수 있다.
1. 포인트 2. 골드

정리하자면...

피스로 사는 게 효율적인 항목
금은2카롱, 노트류 전체

교환소 포인트로 사는 게 효율적인 항목
색2카롱, 색3카롱, 금은1카롱, 금은3카롱, 화분류 전체

빅라이브 골드로 사는 게 효율적인 항목
없음. 단, 금은2카롱은 피스와 효율 차이가 별로 없음.

빅라이브 골드로 사는 게 효율적인 항목이 하나도 없다.

그럼 빅라이브 골드로는 색1카롱을 사는 게 제일 효율적이라는 의미가 되나?

쓸데없이 길게 됐는데, 혹시 수학 잘 하는 사람이 있으면 이 내용 중에 오류가 있는지 좀 봐줬으면 한다.

다시 한 번 강조하는데 난 수학을 못해서 계산의 전제부터 잘못 세웠을 수도 있거든...